Màrius

Avui parlarem d’un dels mètodes (els informàtics en diem algorismes) per fer que un ordinador jugui correctament als escacs, al tres en ratlla, les dames o jocs similars.

Tots hem sentit o vist a les notícies d’ordinadors que ja son grans mestres d’escacs, o no fa gaire, un ordinador de Google va guanyar al millor jugador de Go del món.

El primer que ens cal, es que el joc sigui de dos jugadors i es faci per torns, és a dir, a cada torn juga un dels jugadors, al següent torn juga l’altre jugador, i així van fent fins que un dels dos guanya la partida o tots dos empaten. 

La segona cosa que ens caldrà és un mètode per donar una puntuació a una situació concreta del joc. Si estem jugant a escacs, aquest mètode pot tenir en compte el nombre de peces, el valor que tenen, on està situada cada una, etc.

El mètode (o algorisme) per jugar es coneix com minimax, i el que fa és explorar totes les possibilitats futures (fins a un cert nivell), valorar cada una per separat i llavors veure quines perjudiquen més a l’adversari i afavoreixen a ell mateix.

Aquest algorisme va ser proposat per John von Neumann al 1928 i va ser l’inici del que es coneix com teoria de jocs.

Veiem-ho amb un exemple senzill: jugarem al tres en ratlla.

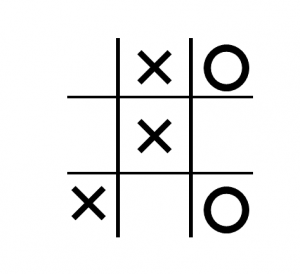
Imaginem que tenim la situació de la figura i que l’ordinador juga amb els cercles:

Situació inicial

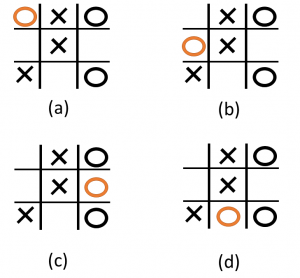
En aquest cas, el jugador cercle te les següents possibles jugades:

Com podem veure ràpidament, la opció (c) és la millor (fa que guanyem la partida!) per tant és la que li hauriem de donar més puntuació.

Tenir una funció que ens digui quina és la millor jugada a fer sembla senzill en alguns casos (com al tres en ratlla), però no sembla gaire possible amb jocs més complexos com els escacs. Què cal fer llavors?

El que cal fer és anar mirant totes les jugades que farà el nostre adversari a continuació i valorar tot el conjunt per poder triar la millor jugada. El que haurem de fer llavors, és agafar la mínima puntuació quan sigui la jugada del rival i agafar la millor puntuació quan sigui la nostra jugada, si podem anar mirant endavant fins veure el final de la partida, millor! Veiem-ho amb un exemple:

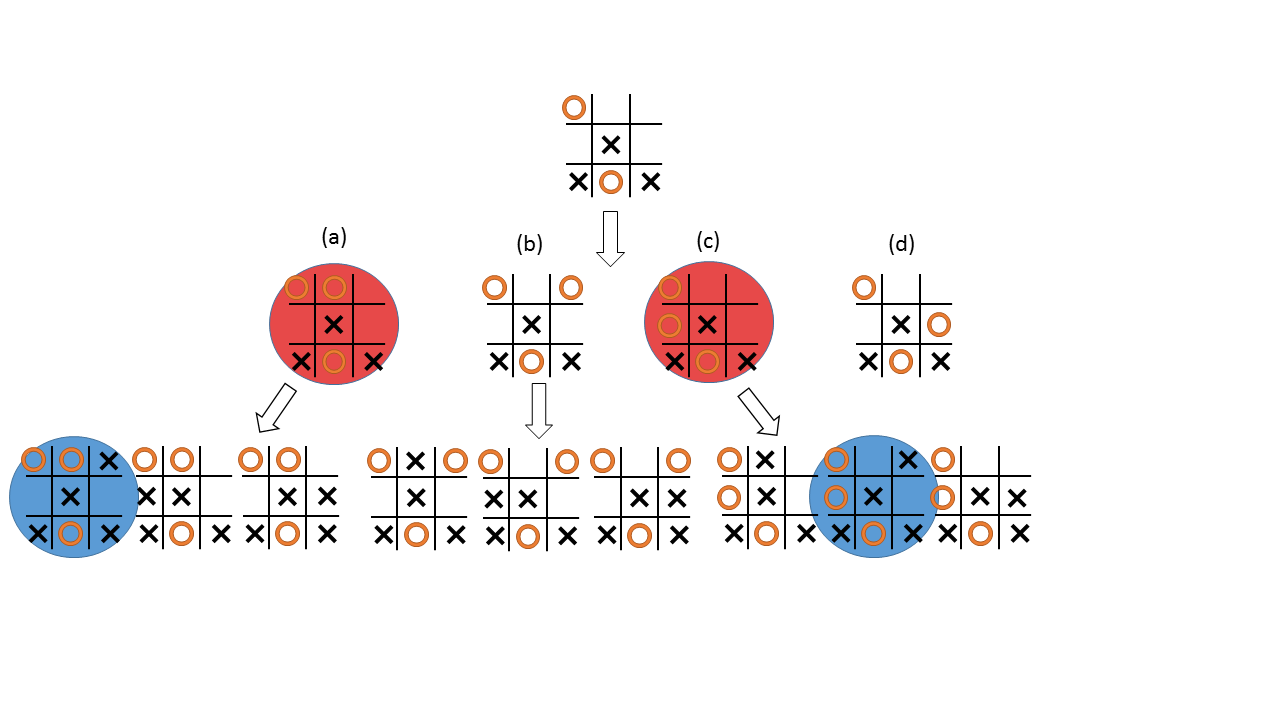
En aquesta situació que es veu al diagrama, el jugador creus acaba de jugar. Quina jugada hauria de fer el jugador dels cercles?

Pica la imatge per ampliar

Donat el tauler tal com està dalt del diagrama, el jugador cercles te 4 possibilitats (etiquetades a, b,c o d). El que farà l’ordinador és mirar les següents jugades possibles (el tercer i últim nivell del diagrama).

Què es veu en aquest últim nivell? Que si el jugador cercles tria les opcions (a) o (c), el jugador creus podrà guanyar la partida (les jugades marcades amb el cercle blau, les jugades de l’opció (d) no estan dibuixades però també guanya el jugador creus). Per tant, què ha de fer el jugador cercles? doncs triar l’opció (b  on, almenys, s’empata, que en el tres en ratlla és el més habitual).

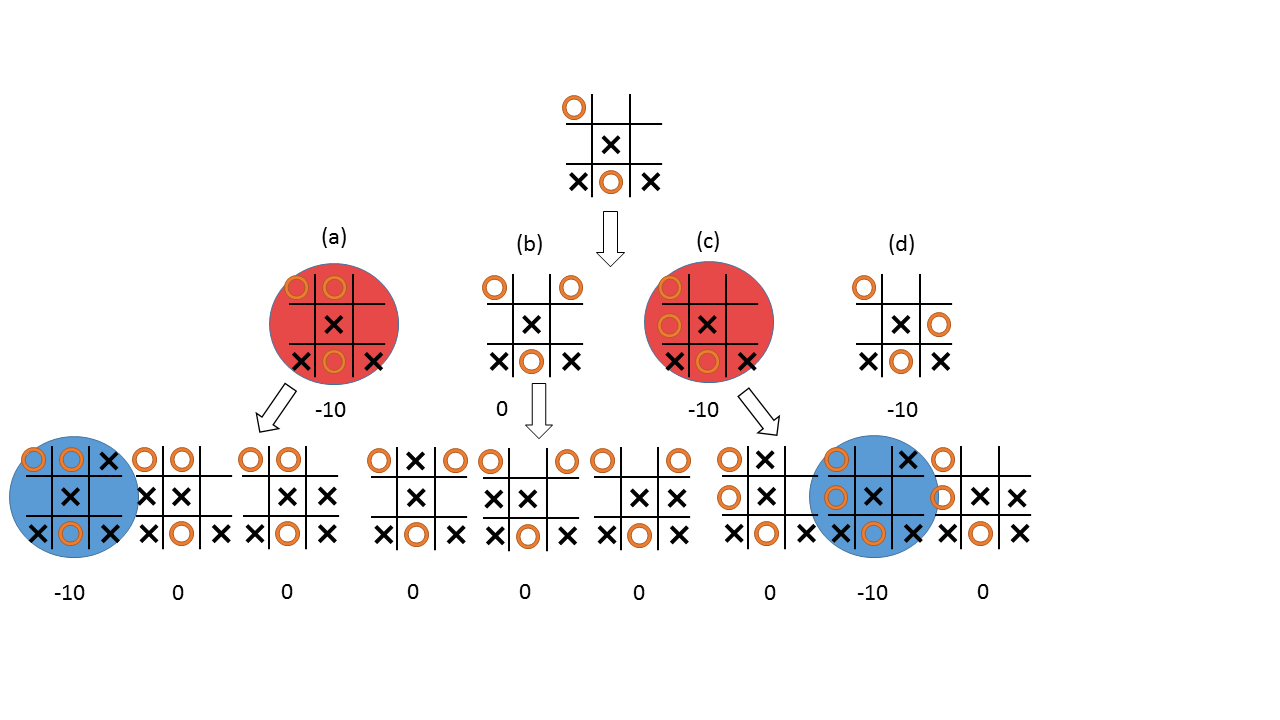
Com farà aquest procés l’ordinador? Doncs donant puntuacions a les posicions de l’últim nivell, mirant qui guanya o si s’empata i donant puntuacions. Com que juguem amb els cercles, posarem +10 si guanyem, 0 si empatem i -10 punts si guanyen les creus.

Pica la imatge per ampliar

Per puntuar el segon nivell, per cada jugada triem la mínima puntuació de cada un de les jugades que li van després. Així tenim que la opció (a) té una puntuació de -10 per que a continuació perdrem a la següent jugada, l’opció (b) té 0 punts i la (c) i (d) tenen -10 punts. Com que hem d’agafar el màxim d’aquestes jugades (0) l’opció que triarà l’ordinador serà l’opció (b). Així doncs, aquesta serà la jugada que farà l’ordinador quan es trobi aquesta situació al tauler.

Senzill, oi? Doncs amb la majoria de jocs aquest sistema funciona i és el que es fa servir. La gràcia de fer un ordinador que jugui millor o pitjor serà dissenyar una manera més bona de puntuar el tauler o de fer que busqui en totes les possibilitats d’una forma més ràpida i coses així.

Limitacions

Cal tenir en compte que per jocs més complicats, com per exemple els escacs, les possibles jugades donada una situació concreta normalment és enorme (de l’ordre de milers de milions de possibilitats!) i que els ordinadors son potents però no tant.

Llavors  el que es fa és no intentar generar totes les possibilitats si no intentar generar a priori bones jugades, ja sigui buscant en partides històriques o amb distintes tècniques d’intel·ligència Artificial com les xarxes neurals o bé intentant arribar a un nombre limitat de jugades endavant i fer suposicions del que pot passar després (funcions heurístiques).

Aquestes funcions el que fan és donar una puntuació sobre la situació del tauler sense que la partida hagi acabat. En el cas dels escacs, podem imaginar una funció heurística que compti el nombre de peons, alfils, cavalls, etc. i segons el nombre de cada peça ens doni un valor de la potència de cada jugador.

Us deixo una animació de com es van generant les puntuacions a cada nivell per que us quedi més clar.

Animació mostrant com funciona MiniMax.
Maschelos at English Wikipedia [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0) or GFDL (http://www.gnu.org/copyleft/fdl.html)], via Wikimedia Commons

Per saber-ne més

• Viquipèdia Minimax 
• Viquipèdia Teoria de jocs
• Viquipèdia John von Neumann